ARBOLES

4.1.1.- CONCEPTO DE ÁRBOL

En ciencias de la informática, un árbol es una estructura de datos ampliamente usada que imita la forma de un árbol (un conjunto de nodos conectados). Un nodo es la unidad sobre la que se construye el árbol y puede tener cero o más nodos hijos conectados a él. Se dice que un nodo  es padre de un nodo  si existe un enlace desde  hasta  (en ese caso, también decimos que  es hijo de ). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.

4.1.2 CLASIFICACIÓN DE ARBOLES

1.- Árboles Binarios

               1.1- Árbol de búsqueda binario auto-balanceable

                    1.2.- Árboles AVL

                   1.3.- Árboles Rojo-Negro

                   1.4.- Árbol AA

  2.- Árboles Multicamino

              2.1.Árboles B (Árboles de búsqueda multicamino autobalanceados)

                    2.2.- Árbol-B+

                    2.3.- Árbol-B*

ARBOLES BINARIOS

En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno.

Tipos de árboles binarios

·         Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.

·         Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.

·         Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura).

·         A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un árbol binario completo como un árbol binario lleno en el que todas las hojas están a profundidad n o n-1, para alguna n.

Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho.

ÁRBOL BINARIO DE BÚSQUEDA AUTO-BALANCEABLE

En ciencias de la computación, un árbol binario de búsqueda auto-balanceable oequilibrado es un árbol binario de búsqueda que intenta mantener su altura, o el número de niveles de nodos bajo la raíz, tan pequeños como sea posible en todo momento, automáticamente.

ÁRBOL AVL 

Árbol avl es un tipo especial de árbol binario ideado por los matemáticos rusos Adelson-Velskii y Landis. Fue el primer árbol de búsqueda binario auto-balanceable que se ideó.

ÁRBOL ROJO-NEGRO

Un árbol rojo-negro es un tipo abstracto de datos. Concretamente, es un árbol binario de búsqueda equilibrado, una estructura de datos utilizada eninformática y ciencias de la computación.

Es complejo, pero tiene un buen peor caso de tiempo de ejecución para sus operaciones y es eficiente en la práctica. Puede buscar, insertar y borrar en un tiempo O(log n), donde n es el número de elementos del árbol.

ÁRBOL AA

En informática un árbol AA es un tipo de árbol binario de búsqueda auto-balanceable utilizado para almacenar y recuperar información ordenada de manera eficiente. Los árboles AA reciben el nombre de su inventor, Arne Andersson.

Los árboles AA son una variación del árbol rojo-negro, que a su vez es una mejora del árbol binario de búsqueda. A diferencia de los árboles rojo-negro, los nodos rojos en un árbol AA sólo pueden añadirse como un hijo derecho. En otras palabras, ningún nodo rojo puede ser un hijo izquierdo. De esta manera se simula un árbol 2-3 en lugar de un árbol 2-3-4, lo que simplifica las operaciones de mantenimiento. Los algoritmos de mantenimiento para un árbol rojo-negro necesitan considerar siete diferentes formas para balancear adecuadamente el árbol:

En un árbol AA, al cumplirse el estricto requisito de que sólo los enlaces derechos pueden ser rojos, sólo es necesario considerar dos formas:

ÁRBOL MULTICAMINO

Los árboles multicamino o árboles multirrama son estructuras de datos de tipo árbol usadas en computación.

Un árbol multicamino posee un grado g mayor a dos, donde cada nodo de información del árbol tiene un máximo de g hijos.

ÁRBOL-B 

En las ciencias de la computación, los árboles-B o B-árboles son estructuras de datos de árbol que se encuentran comúnmente en las implementaciones de bases de datos y sistemas de archivos. Son árboles balanceados de búsqueda en los cuales cada nodo puede poseer más de dos hijos. Los árboles B mantienen los datos ordenados y las inserciones y eliminaciones se realizan en tiempo logarítmico amortizado.

Árbol B+

En ciencias de la computación, un árbol B+ es un tipo de estructura de datos de árbol, representa una colección de datos ordenados de manera que se permite una inserción y borrado eficientes de elementos. Es uníndice, multinivel, dinámico, con un límite máximo y mínimo en el número de claves por nodo. Un árbol B+ es una variación de un árbol B.

En un árbol B+, toda la información se guarda en las hojas. Los nodosinternos sólo contienen claves y punteros. Todas las hojas se encuentran en el mismo nivel, que corresponde al más bajo. Los nodos hoja se encuentran unidos entre sí como una lista enlazada para permitir búsqueda secuencial.

Árbol-B*

Un árbol-B* es una estructura de datos de árbol, una variante de Árbol-B utilizado en los sistemas de ficheros HFS y Reiser4, que requiere que los nodos no raíz estén por lo menos a 2/3 de ocupación en lugar de 1/2. Para mantener esto los nodos, en lugar de generar inmediatamente un nodo cuando se llenan, comparten sus claves con el nodo adyacente. Cuando ambos están llenos, entonces los dos nodos se transforman en tres. También requiere que la clave más a la izquierda no sea usada nunca.

No se debe confundir un árbol-B* con un árbol-B+, en el que los nodos hoja del árbol están conectados entre sí a través de una lista enlazada, aumentando el coste de inserción para mejorar la eficiencia en la búsqueda.

4.1.3 OPERACIONES BÁSICAS SOBRE ARBOLES BINARIOS

▪Enumerar todos los elementos.

▪Buscar un elemento.

▪Dado un nodo, listar los hijos (si los hay).

▪Borrar un elemento.

▪Eliminar un subárbol (algunas veces llamada podar).

▪Añadir un subárbol (algunas veces llamada injertar).

▪Encontrar la raíz de cualquier nodo.

Por su parte, la representación puede realizarse de diferentes formas. Las más utilizadas son:

▪Representar cada nodo como una variable en el heap, con punteros a sus hijos y a su padre.

▪Representar el árbol con un array donde cada elemento es un nodo y las relaciones padre-hijo vienen dadas por la posición del nodo en el array.

4.1.4 APLICACIONES

Los arboles binarios facilitan la búsqueda y ordenamiento de los datos de alta velocidad, la eliminación eficiente de elementos de datos duplicados, la representación de directorios del sistema de archivos y la compilación de expresiones en lenguaje maquina.

 Él árbol de búsqueda binaria facilita la eliminación de valores duplicados. Al crear un árbol se reconocen los intentos de insertar un valor duplicado, ya que este sigue las mismas decisiones de “ir a la izquierda” o “ir a la derecha” en cada comparación, al igual que el valor original. Por lo tanto, eventualmente se comprar el valor duplicado con un nodo que contenga el mismo valor. El valor duplicado puede destacarse en este punto.

Otra de las aplicaciones más importantes es dentro de la inteligencia artificial, y más concretamente en el área de reconocimiento de patrones. Se trata de utilizar los arboles para realizar clasificaciones. La clave está en asignar a cada nodo del árbol un significado. Las distintas ramas tienen asociados criterios que ayudan a determinar el sentido de las búsquedas.

También con aplicables en el análisis de notaciones algebraicas y la implementación de algoritmos de compresión, etc.

4.1.5 Arboles balanceados (AVL).

Árbol balanceado AVL

La principal característica de estos es la de realizar reacomodos o balanceos, después de inserciones o eliminaciones de elementos.

Estos árboles también reciben el nombre de AVL (autores: 2 matemáticos rusos G.M. Adelson-Velskii y E.M Landis en1962).

Formalmente se define un árbol balanceado como un árbol de búsqueda, en el cual se debe cumplir la siguiente condición: “Para todo nodo T del árbol la altura de los subárboles izquierdo y derecho no deben diferir en a lo sumo una unidad”.

Definición:

Básicamente un árbol AVL es un Árbol Binario de Búsqueda al que se le añade una condición de equilibrio.

“Para todo nodo la altura de sus

subárboles izquierdo y derecho

pueden diferir a lo sumo en 1”.

Gracias a esta forma de equilibrio (o balanceo), la complejidad de una búsqueda en uno de estos árboles se mantiene siempre en orden de complejidad O(log n).

Condición de equilibrio

“Para todos los nodos, la altura de la rama

izquierda no difiere en más de una unidad

de la altura de la rama derecha”

Estructuras de datos

30 Árbol balanceado AVL

Características

* Un AVL es un ABB.

* La diferencia entre las alturas de los subárboles. derecho e izquierdo no debe excederse en más de 1.

* Cada nodo tiene asignado un peso de acuerdo a las alturas de sus subárboles.

* Un nodo tiene un peso de 1 si su subárbol derecho es más

          alto, -1 si su subárbol izquierdo es más alto y 0 si las alturas son las mismas.

* La inserción y eliminación en un árbol AVL es la misma que en un ABB.

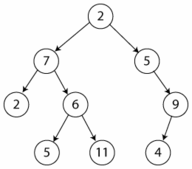
Ejemplo de AVL

Sólo el árbol de la izquierda es AVL. El de la derecha viola la condición de equilibrio en el nodo 6, ya que su subárbol izquierdo tiene altura 3 y su subárbol derecho tiene altura 1.

Grafo (estructura de datos)

Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.

Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.

Formas de representación

Existen diferentes implementaciones del tipo grafo: con una matriz de adyacencias (forma acotada) y con listas y multilistas de adyacencia (no acotadas).

o Matriz de adyacencias: se asocia cada fila y cada columna a cada nodo del grafo, siendo los elementos de la matriz la relación entre los mismos, tomando los valores de 1 si existe la arista y 0 en caso contrario.

o Lista de adyacencias: se asocia a cada nodo del grafo una lista que contenga todos aquellos nodos que sean adyacentes a él.

Especificación de los tipos abstractos de datos de un grafo no dirigido

Generadores

Crear un grafo vacío: Devuelve un grafo vacío. 

* op crearGrafo: -> Grafo [ctor].

Añadir una arista: Dado un grafo, añade una relación entre dos nodos de dicho grafo.

* op añadirArista: Grafo Nodo Nodo -> [Grafo] [ctor].

Añadir un nodo: Dado un grafo, incluye un nodo en él, en caso en el que no exista previamente. 

* op añadirNodo: Grafo Nodo -> Grafo [ctor].

Constructores

Borrar nodo: Devuelve un grafo sin un nodo y las aristas relacionadas con él. Si dicho nodo no existe se devuelve el grafo inicial.

* op borrarNodo: Grafo Nodo -> Grafo.

Borrar arista: Devuelve un grafo sin la arista indicada. En caso de que la arista no exista devuelve el grafo inicial.

* op borrarArista: Grafo Nodo Nodo -> Grafo.

Selectores

Grafo Vacio: Comprueba si un grafo no tiene ningún nodo.

* op esVacio: Grafo -> Bool.

Contener Nodo: Comprueba si un nodo pertenece a un grafo.

* op contiene: Grafo Nodo -> Bool.

Adyacentes: Comprueba si dos nodos tienen una arista que los relacione.

* op adyacentes: Grafo Nodo Nodo -> Bool.

Para la especificación de un grafo dirigido tenemos que modificar algunas de las ecuaciones de las operaciones borrarArista y añadirArista para que no se considere el caso de aristas bidireccionales.

Y sustituir la operación adyacentes por:

* op predecesor: Grafo Nodo Nodo -> Bool.

* op sucesor: Grafo Nodo Nodo -> Bool.

4.2.- GRAFOS

Un grafo G es k-colorable si admite una coloración con k colores. Al menor k tal que G es k-colorable se le llama número cromático de G y se denota ­(G). Obviamente todo grafo de orden n es n-colorable. Kn no se puede colorear con menos de n colores, pues como todos sus vértices son adyacentes cada uno debe pintarse de un color diferente. Por lo tanto ­(Kn) = n. El número cromático de un grafo sin aristas es 1. Un camino de longitud n > 2 tiene número cromático 2, ya que sus vértices pueden pintarse con dos colores en forma alternada, comenzando por un extremo.

Polinomios Cromáticos

Definición: Dado un grafo G y un número natural x, llamemos PG(x) al número de coloraciones por vértices de G con colores {1, 2, . . . , x}. A PG(x) se le llama polinomio cromático de G, ya que como veremos siempre es un polinomio en x.

Ejemplo: hallar el polinomio cromático del grafo G

Se comienza por asignar al vértice a uno cualquiera de los x colores disponibles. Ahora b se puede pintar con cualquiera de los x−1 colores restantes; c sólo se puede pintar de x−2 maneras, ya que no puede tener igual color que a ni que b; d se puede pintar con cualquier color diferente al de b, es decir x−1 posibilidades; e se puede pintar con cualquier color diferente al de c, es decir x−1 posibilidades.

Por el principio del producto:

PG(x)=x(x − 1)(x − 2)(x − 1)(x − 1)=x(x − 1)3 (x − 2).

BIBLIOGRAFIA:

1.- dalvycitoxD, arboles binarios y grafos - estructura de datos.wmv, 

Subido el 16/01/2011, dalvycito@perulite.com, http://www.youtube.com/watch?v=4lVopr6ucpY

2.- Wikipedia®, Licencia Creative Commons Atribución Compartir Igual 3.0, modificada por última vez el 29 mayo 2013, a las 17:46. http://es.wikipedia.org/wiki/%C3%81rbol_(inform%C3%A1tica)

3.- http://es.scribd.com/doc/75745434/Unidad-4-Arboles-y-Grafos-OAG-Investigacion-2